מאמר: תגובת מבנים לתנודות קרקע בקרבת שבר

Near field pulse like ground motions

המאמר נכתב במסגרת עבודה מסכמת לתואר שני באוניברסיטת בן גוריון בנגב.

• מנחה: ד"ר רוני קמאי

• סטודנט: לירן פדידה

אחד האתגרים המרכזיים בתחום זה הוא להעריך את הרעידה עצמה - באיזה עוצמה היא תהיה, באיזה תדירות, מתי בכלל צפוי לנו רעידה כזאת או אחרת ומה המרחק של נק' השבר מהמבנה. דבר המקשה עוד על אופי תכנון המבנה ובחירת החומרים והאלמנטים ממנו ייבנה.

במאמר זה נתמקד במרחק של נק' השבר של הרעידה ביחס למבנה, ועל רכיבי כיוון הרעידה (FN ו- FP).

כשבוחנים תנודות קרקע הנבדקות בתחנות שדה הקרובות לאזור שבר, ניתן לראות כי הרעידות מכילות פולסים ברורים בתאוצה, מהירות והזזות המבנה.

עבור אותה תאוצת קרקע (PGA) ומשך הזמן של הרעידה - תנועות קרקע עם פולסים ישירים יכולות ליצור כוחות גזירה בבסיס באופן גבוה בצורה משמעותית, הזזות בין קומות (drifts), והזזות קריטיות בקומות העליונות של בניינים גבוהים. כמו כן, דרישת המשיכות יכולה להיות גבוהה בהרבה והיעילות של מערכת הריסון נמוכה יותר כשמדובר על תנועות קרקע עם פולסים.

למרות ההתקדמות הגדולה בתחום זה, עדיין ישנה אי בהירות רחבה לבעיה זו.

אחד האתגרים המרכזיים הוא להבין באופן ודאי איזה רכיב של הרעידה משפיע יותר במצב זה. השיטה המקובלת בימים אלו היא לקחת את תנודת הקרקע המגיעה לאתר הנבדק ולפרק אותה לשני רכיבי רעידה:

• רכיב מקביל  לכיוון לרעידה (FP).
• רכיב הניצב לכיוון הרעידה (FN) – (ה"נורמל").

במאמר התמקדנו בשני מקורות:

[1] Praveen K. Malhotra, Manuel Archila, Carlos E.(2017)

מאמר המציג תוצאות ממחקרים פרמטריים החוקרים את השפעות הכיווניות על תגובה דינמית לא לינארית של מבנים פשוטים ומבנים גבוהים.

[2] Ventura, W. D. Liam Finn (1999)

מאמר המציג השוואה בין ארבעה רישומים של תנודות קרקע. שלושה רישומים של רעידות אמיתיות שקרו, ורישום נוסף של רעידה "סינתטית" (מעבדתית).

ברעידות עם פולסים, במבנים הקרובים לשבר נצפה כי התנודות משפיעות על התגובה הסיסמית באופן שונה ממבנים המרוחקים מהשבר. ולכן, נסתכל על תנודות קרקע שנצפו קרוב- עד 10 ק"מ ותנודות שנצפו רחוקות יותר.

הרישומים נלקחו מהמאגר של Pacific Earthquake Engineering Research (PEER) Center Ground Motion תחת הפרויקט NGA- פרויקט שפיתח מודלים לחישוב תנודות קרקע, כאשר יש התייחסות גם לרכיבי הרעידה בכיוון המקביל וגם בכיוון הנורמלי (FN FP).

ברכיב הנורמלי ברישום הקרוב ניתן לראות את ההשפעה בזמני מחזור של מעל 2 שניות, מכאן ניתן להסיק שההשפעה הגדולה יותר במצב זה תהיה על מבנים עם זמן מחזור ארוך (מבנים גבוהים, גשרים וכו') מה שייתן במצב הזה הזזות גדולות ומשמעותיות יותר.

גם ברכיב המקביל ניתן לראות את ההשפעה בזמני מחזור של בין 2 עד 4.5 שניות.

כמו כן, ניתן לראות שרכיב הנורמלי הפולס משפיע קצת יותר ובמצב הזה נקבל מהירות גבוה יותר והזזה משמעותית יותר.

ננסה להבין מה היא ההשפעה שלו על מבנים ולמה זה באמת יכול להיות מאוד קריטי לחיי המבנה במקרים מסוימים:

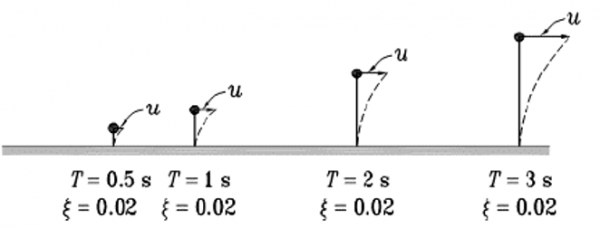
1. הפחתת הגמישות - מבנים מתנהגים בצורה קשיחה או גמישה, תלוי אם הם נמצאים באזור הרגיש להאצה של הספקטרום או מחוצה לו. ככל שרוחב האזור הרגיש לתאוצה רחב יותר, כך גדל מספר המבנים שמתנהגים בצורה קשיחה. לדוגמה, בניין רב קומות גמיש ובניין צמוד קרקע בעל מסה זהה לבניין הרב קומות (מבנה "מסיבי") כך שנקבל את שניהם עם אותו זמן מחזור טבעי ארוך:

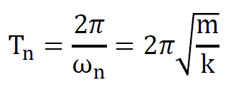לדוגמה מבנים עם זמן מחזור של 2.5 שניות ומעלה ייחשבו כגמישים לתנודות הקרקע של EC וSY, אך קשיחים לתנודת הקרקע הסינתטית.

2. הגברת כוח הגזירה בבסיס המבנה וההזזה הבין קומתית - אזור רגיש להאצה גורם להגברה של מודים בזמני מחזור הארוכים, וכאשר בניינים רבי קומות בעלי זמני מחזור ארוכים נמצאים באזור זה של הספקטרום. מה שגורם גם להגדלת כוח הגזירה בבסיס וגם להזזה בין קומתית.

3. הפחתת התרומה של מודים גבוהים יותר - אזור רגיש להאצה גורם למצב שהמוד הראשון הפועל בבסיס אפילו של בניין גבוה למדי, להישאר באזור זה של הספקטרום. לכן התרומה של המוד הראשון בבסיס עולה בהשוואה לזו של המודים הגבוהים יותר.

4. יעילות מופחתת של מערכות הריסון במבנה – מערכות ריסון יעילות יותר עבור מבנים גמישים, מכיוון שאזור רגיש להאצה גורם למערכות רבות להתנהג בצורה קשיחה זה מצמצם את היתרון של שימוש במערכות אלה.

5. דרישה למשיכות – מקדם הגברת הכוח Rd הוא גבוה יותר עבור מערכות קשיחות שנמצאות באזור של הרגישות לתאוצה.

למרות כל הממצאים, מספר סוגיות הקשורות לתנודות קרקע אימפולסיביות ותגובה סיסמית של מבנים טרם נחקרו באופן נרחב, כולל ההשפעה של כיוון תנודת הקרקע. בהתבסס על אי וודאות לגבי כיוון תנודות הקרקע עלו השאלות הבאות:

1. האם תנודת הקרקע המסובבת בכיוון של FN/FP היא התנודה הקריטית לפגיעה במבנה?

2. האם הכיוון המירבי הוא הקריטי?

3. האם ישנה שיטה יעילה להערכת התגובה הקריטית של מבנה גבוה?

השלבים הבאים יושמו כדי לענות על שאלות אלו:

• ביצוע מחקרים פרמטריים לבחינת השפעת הכיוון של תנודות הקרקע על התגובה הדינאמית של מערכות בעלות דרגת חופש אחת  (SDOF). משתני הפולס, משך זמן המחזור שלו, ועוד נתונים על ידי שימוש בפולסים סינתטיים המייצגים את הפולסים הכלולים ברשומות של תנודת קרקע. על סמך תוצאות מחקר זה מוצעת שיטה להערכת ההזזה הקריטית במבנה.
• בחירה של קבוצת תנודות קרקע הקרובות לנק' השבר המייצגות תרחישים של רעידות אדמה.
• קביעת תלות האוריינטציה של האמפליטודה ומשך זמן המחזור עבור המהירות של הפולסים הכלולות ברשומות שנבחרו.
• אנליזה ישירה מתבצעת באמצעות מודל לא-ליניארי תלת-ממדי של בניין גבוה כדי לקבוע את תגובת ההזזה הקריטית לתנודות האדמה עם פולסים שנבחרו. תנודות האדמה מסתובבות עם כיוון השעון בזוויות במדרגות של חמש מעלות כל פעם, בטווח של בין 0 מעלות עד 180 מעלות. תגובת ההזזה הקריטית מוגדרת כמעטפת התגובות המחושבות מניתוחים מרובים לתנודות קרקע מסתובבות.
• השוואות מבוצעות בין תגובת ההזזה הקריטית והתגובות לתנודות קרקע מסתובבות ספציפיות כדי לקבוע איזה קלט יכול לספק באופן אמין הערכה טובה של תגובת ההזזה הקריטית.
• חקירת תגובת ההזזה הקריטית לאורך ציר מבני יחיד של בניין גבוה הנתון לתנודות קרקע דו-כיווניות.

המטרה לזהות את המאפיינים של האמפליטודה וזמני המחזור של הפולסים הסינתטיים שהובילו לתגובת ההזזה הקריטית של המבנה. הרצון מאחורי גישה זו היה כי אם נוכל לזהות את המאפיינים של האמפליטודה ברגעים אלו נוכל להציע גבולות למשך הפולס ולגודל האמפליטודה כדי להעריך את התגובה הקריטית של מבנים גבוהים כאשר ה- NRHA מתבצע באמצעות רשומות של תנודות קרקע בעלי פולסים אלו.

המודל החישובי של מערכות בעלת דרגת חופש אחת היא כמו שאנחנו מכירים מדינמיקת מבנים,

מסה המחוברת לקפיץ אלסטו-פלסטי בעל מקדם קשיחות K וחסר משקל ולמערכת ריסון בעלת מקדם ריסון C וחסרת משקל

משוואת תנועה דיפרנציאלית זו נפתרה נומרית בשיטת ההאצה הממוצעת של ניומרק (Newmark's average acceleration method) עם β = 0.25 ו- γ = 0.5. ריסון טבעי של 5% והתנאים ההתחלתיים היו במנוחה. תזוזת השיא נקבעה כערך המוחלט המרבי מהיסטוריית התגובות.

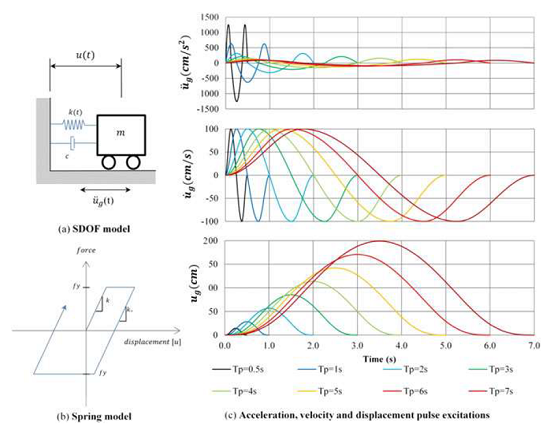
איור - מודל עבור מערכת SDOF והצגה גרפית כאשר Tp- משך הפולס

תגובות ההזזה לשיא עבור המערכת עם זמן מחזור אלסטי של 2 שניות לפולסים של אמפליטודת מהירות שיא אחידה מוצגים באיור 10, כאשר מוצגים בשלושה גרפים בשלושה מהירויות שונות 40,100,150 ס"מ/שנייה בהתאמה . הציר התחתון האופקי מציג את היחס Tp / T והציר העליון האופקי מראה את משך הפולס Tp. כאן אנו מגדירים את משך הפולס המהיר כפרק הזמן של מחזור תנודת קרקע אחד בסדרת הזמן המהיר. נציין כי הזזות השיא הגדולות ביותר מתרחשות תמיד כאשר משך הפולס ארוך יותר מזמן מחזור האלסטי של המערכת (Tp / T> 1). ככל שהאמפליטודה של הפולס גדלה, התגובה עולה; והיחס Tp / T שמוביל להזזה הגבוהה ביותר עולה גם כן. עבור Tp / T <<1 או Tp / T>> 1, התגובות קטנות וכמעט זהות לכל המערכות.

כאשר -

• משך הפולס Tp-
• זמן המחזור של המוד הראשון T-
• נק' הכניעה המנורמל Cy-

על מנת להעריך את ההזזה הקריטית במבנים גבוהים החוקרים Manuel Archila, Carlos E. Ventura,   W. D. Liam Finn(2017)[2]  הציעו את הדבר הבא:

(א) להכיל פולסי מהירות אשר משך זמן המחזור שלהם ארוך יותר מהזמן מחזור של המבנה במוד הראשון.

(ב) האמפליטודה של פולס המהירות צריכה להיות המקסימאלית בין כל כיווני תנודת הקרקע.

לפי הצעה זו, אנו רואים שהם מייחסים חשיבות גם לכיווני רכיבי הרעידה שמגיעים לאתר וגם לספקטרום התגובה של המבנה הספציפי, וזה בעצם שילוב של כל מה שאנחנו מנסים לעשות במאמר הזה. ושיטה זו עונה על כל התצפיות שלנו.

 עבור רשומה נתונה, רכיב תנודת הקרקע העונה על קריטריון כפול זה נקרא תנודת קרקע CMV. השלבים הבאים תוחמים את שיטת CMV המוצעת:

שלב 1 - נקבע את זמן המחזור של המבנה במוד הראשון , לאורך הציר המבני בו אמורים להעריך את תגובת הזזה הקריטית.

שלב 2 - נקבע את תלות האוריינטציה של זמן המחזור של הפולס במהירות בטווח שבין 0 ° ל- 180 °.

שלב 3 - ניקח רק פולסים בעלי משך זמן Tp ארוך מ- T. מפולסים אלו יש לזהות את האוריינטציה של המהירות המרבית, שהופכת לכיוון של המהירות המרבית. בשלב זה - אם אף אחד מהפולסים לא עומד בקריטריון הכפול הזה, מומלץ לבחור ברשומה של תנודת קרקע אחרת.

שלב 4 - נסובב את הצמד כדי ליישר את תנודת הקרקע המהירות המרבית משלב 3 עם הציר המבני בשלב 1.

שלב 5 - נחשב את התגובה הסיסמית הלא לינארית לזוג תנודות הקרקע משלב 4.

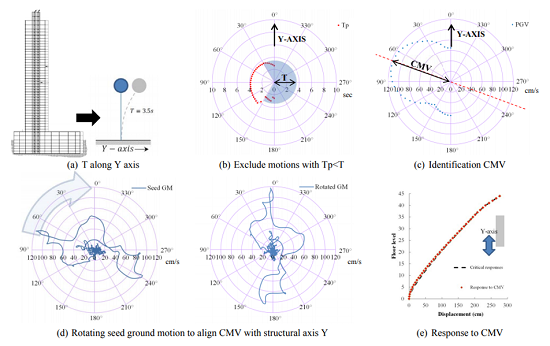
איור - המחשה גרפית לביצוע השלבים CMV

שיטת CMV הוחלה על מערכות בעלות דרגת חופש אחת (SDOF) באמצעות 45 רשומות בקרבת האתר וסיפקה קירובים טובים לתגובת ההזזה הקריטית, דיון בהרחבה בנושא ניתן לראות במאמר ב- M. Archila(2014)[19].

ניתן לראות את תגובת ההזזה הקריטית בשיטת CMV לעומת שיטת האנליזה הישירה למצב שבו נק' הכניעה המנורמלת שווה ל-0.15 (Cy) וזמן המחזור הינו 3 שניות כאשר בציר X התחתון אנו רואים את ההזזה בשיטת CMV בס"מ ובציר Y השמאלי רואים את ההזזה בשיטת האנליזה הישירה בס"מ.

ניתן לראות את הסטייה בין שני החישובים, נציין ששיטת האנליזה הישירה היא שיטה מאוד יקרה ביחס לשיטת CMV.

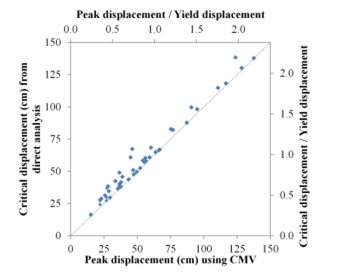
איור- השוואה של תוצאות בין שיטת CMV לבין אנליזה ישירה עבור T=3 Cy=0.15

בטבלה הבאה ניתן לראות את אחוז השגיאה שיצא בחישוב בין שיטתCMV  לשיטת האנליזה הישירה כאשר הבדיקה נעשתה לשלושה מצבים של נק' הכניעה המנורמלת (Cy=0.15;0.20;0.25) ולשלושה זמני מחזור שונים לכל נק' (T=1;2;3) ואת השגיאה חישבו באופן הבא:

באופן כללי אנו רואים שאחוז השגיאה בכל המצבים הוא שולי (ביחס למשקל הכלכלי של כל שיטה). כמו כן, אפשר לומר שככל שזמן המחזור ארוך יותר מקבלים דיוק גבוה יותר - מה שאומר שבמבנים גבוהים אחוז השגיאה יהיה קטן יותר. ןזה מה שמעיד על יעילות השיטה.

לסיכום, באזורים בהם יש סכנה לקבלת פולסים אלו- האתרים הנמצאים בקרבת השבר מצויים בסכנה גבוהה, ויש לקחת בחשבון את הגישות החישוביות וההשפעות על המבנה.

צריך לקחת בחשבון בתכנון כל מבנה באשר הוא, הם ערכי המקס' של תאוצה, מהירות והזזה (PGA, PGV, PGD), ערכים אלה הינם המפתח העיקרי לשליטה בכל מאפייני התכנון במבנים אשר מושפעים מתנודות בקרבת השבר ולתכן של מבנים לתגובות סייסמיות.

מקורות מידע

1. Response of buildings to near‐field pulse‐like ground motion, Praveen K. Malhotra

2. New insights on effects of directionality and duration of near‐field ground motions on seismic response of tall buildings, Manuel Archila, Carlos E. Ventura,   W. D. Liam Finn

3. J. P. Singh, The influence of seismic source directivity on strong ground motion, Ph.D. dissertation, Berkeley, Calif: University of California, COMTEX Scientific Corporation, N.Y., 1 – 183, 1981.

4. P. G. Somerville, N. F. Smith, R. W. Graves, N. A. Abrahamson, Seismol. Res. Lett. 1997, 68 ( 1 ), 199.

5.K. J. Howard, C. A. Tracy, R. G. Burns, Earthq. Spectra 2005, 21 ( 4 ), 1063.

6. J. A. Watson‐Lamprey, D. M. Boore, Beyond Sa GMRotI : Conversion to Sa Arb, Sa SN and Sa MaxRot, Bull. Seismol. Soc. Am. 2007, 97 ( 5 ), 1511

7. S. K. Shahi, J. W. Baker, Preliminary NGA‐West 2 models for ground‐motion directionality. Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, 2012

8. Y. N. Huang, A. S. Whittaker, N. Luco, Earthq. Spectra 2008, 24 ( 1 ), 319.

9. N. M. Newmark and W. J. Hall, &Earthquake spectra and design1, Earthquake Engineering Research Institute, Oakland,CA, 1982

10. Chopra, Anil K. Dynamics of Structures : Theory and Applications to Earthquake Engineering. 3rd ed. Upper Saddle River, N.J.: Pearson/Prentice-Hall, 2007. Print. Prentice-Hall International Ser. in Civil Engineering and Engineering Mechanics.

11. A. Rigato, R. Medina, Eng. Struct. 2007, 29 ( 10 ), 2593

12. J. C. Reyes, E. Kalkan, Relevance of fault‐normal/parallel and maximum direction rotated ground motions on nonlinear behavior of multi‐story buildings. Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, 2012.

13. N. Lagaros, Struct. Infrastruct. Eng. 2010, 6 ( 2 ), 77.

14. M. Archila, C. E. Ventura, Effect of ground motion directionality on seismic response of tall buildings. Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, 2012

15. A. S. Veletsos, N. M. Newmark, Response spectra of single degree‐of‐freedom elastic and inelastic systems. Design Procedures for Shock Isolation Systems of Underground Protective Structures, Report RTD TDR‐63‐3096, Vol. III, Air Force Weapons Laboratory, Kirtland Air Force Base, New Mexico, 1964.

16. N. N. Ambraseys, Maximum intensity of ground movement caused by faulting. Proceedings of the Fourth World Conference on Earthquake Engineering. Santiago de Chile 1969, 154 – 171.

17. J. N. Brune, J. Geophys. Res. 1970, 75 ( 26 ), 4997.

19. M. Archila. Directionality effects of pulse‐like near‐field ground motions on seismic response of tall buildings. PhD Dissertation, The University of British Columbia, British Columbia, Canada 2014, 1 – 177.